Large Language Models

Refer to the amazing 3blue1brown video explaining transformer neural networks.

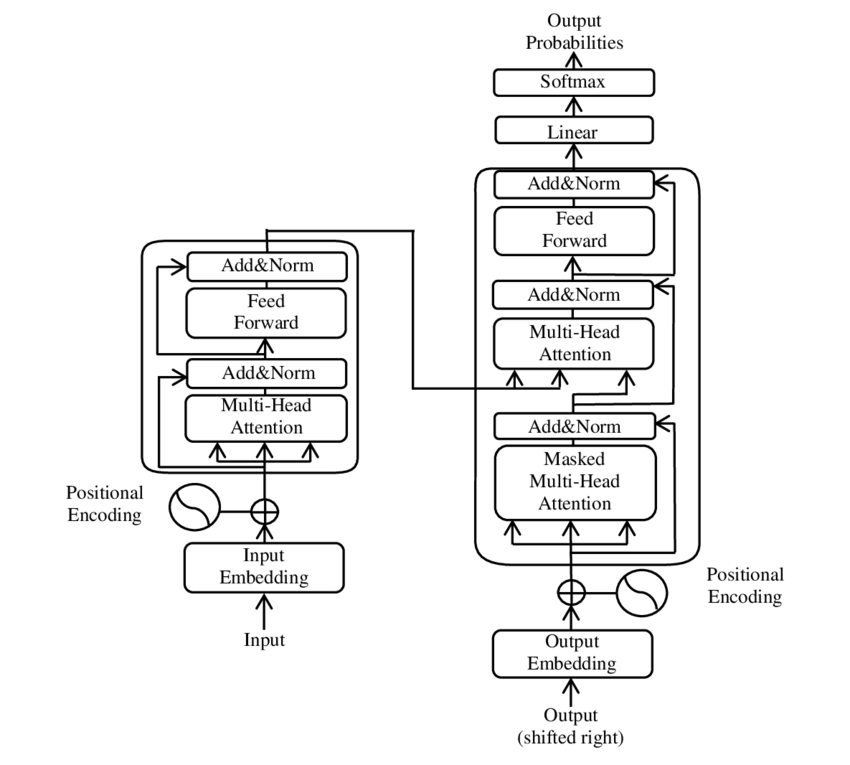
The transformer network

The softmax equation

In the same way that you might call the components of the output ( $σ (x)_{i}$ ) of this function probabilities, people often refer to the inputs ( $x$ ) as logits.

$\begin{matrix} (22.1) & σ (x)_{i} = \frac{e^{x_{j}}}{\sum_{j = 1}^{n} e^{x_{j}}} \end{matrix}$

Adding randomness with the temperature parameter

In some situations, like when ChatGPT is using this distribution to create a next word, there’s room for a little bit of extra fun by adding a little extra spice into this function, with a constant $T$ thrown into the denominator of those exponents.

$\begin{matrix} (22.2) & σ (x)_{i} = \frac{e^{x_{j} T^{- 1}}}{\sum_{j = 1}^{n} e^{x_{j} T^{- 1}}} \end{matrix}$

We call it the temperature, since it vaguely resembles the role of temperature in certain thermodynamics equations, and the effect is that when $T$ is larger, you give more weight to the lower values, meaning the distribution is a little bit more uniform, and if $T$ is smaller, then the bigger values will dominate more aggressively, where in the extreme, setting $T$ equal to zero means all of the weight goes to maximum value.

For example, I’ll have GPT-3 generate a story with the seed text, once upon a time there was A, but I’ll use different temperatures in each case. Temperature zero means that it always goes with the most predictable word, and what you get ends up being a trite derivative of Goldilocks. A higher temperature gives it a chance to choose less likely words, but it comes with a risk.